A second-order segment in the plane or in 3D space. More...

#include <lf/geometry/segment_o2.h>

Inheritance diagram for lf::geometry::SegmentO2:

Public Member Functions
	SegmentO2 (Eigen::Matrix< double, Eigen::Dynamic, 3 > coords)
	Constructor building segment from vertex/midpoint coordinates. More...

dim_t	DimLocal () const override
	Dimension of the domain of this mapping. More...

dim_t	DimGlobal () const override
	Dimension of the image of this mapping. More...

base::RefEl	RefEl () const override
	The Reference element that defines the domain of this mapping. More...

Eigen::MatrixXd	Global (const Eigen::MatrixXd &local) const override
	Map a number of points in local coordinates into the global coordinate system. More...

Eigen::MatrixXd	Jacobian (const Eigen::MatrixXd &local) const override
	Evaluate the jacobian of the mapping simultaneously at `numPoints` points. More...

Eigen::MatrixXd	JacobianInverseGramian (const Eigen::MatrixXd &local) const override
	Evaluate the Jacobian * Inverse Gramian ( \( J (J^T J)^{-1}\)) simultaneously at `numPoints`. More...

Eigen::VectorXd	IntegrationElement (const Eigen::MatrixXd &local) const override
	The integration element (factor appearing in integral transformation formula, see below) at number of evaluation points (specified in local coordinates). More...

std::unique_ptr< Geometry >	SubGeometry (dim_t codim, dim_t i) const override
	Construct a new Geometry() object that describes the geometry of the `i`-th sub-entity with codimension=`codim` More...

std::vector< std::unique_ptr< Geometry > >	ChildGeometry (const RefinementPattern &ref_pat, base::dim_t codim) const override
	Generate geometry objects for child entities created in the course of refinement. More...

Public Member Functions inherited from lf::geometry::Geometry
virtual dim_t	DimLocal () const =0
	Dimension of the domain of this mapping. More...

virtual dim_t	DimGlobal () const =0
	Dimension of the image of this mapping. More...

virtual base::RefEl	RefEl () const =0
	The Reference element that defines the domain of this mapping. More...

virtual Eigen::MatrixXd	Global (const Eigen::MatrixXd &local) const =0
	Map a number of points in local coordinates into the global coordinate system. More...

virtual Eigen::MatrixXd	Jacobian (const Eigen::MatrixXd &local) const =0
	Evaluate the jacobian of the mapping simultaneously at `numPoints` points. More...

virtual Eigen::MatrixXd	JacobianInverseGramian (const Eigen::MatrixXd &local) const =0
	Evaluate the Jacobian * Inverse Gramian ( \( J (J^T J)^{-1}\)) simultaneously at `numPoints`. More...

virtual Eigen::VectorXd	IntegrationElement (const Eigen::MatrixXd &local) const =0
	The integration element (factor appearing in integral transformation formula, see below) at number of evaluation points (specified in local coordinates). More...

virtual std::unique_ptr< Geometry >	SubGeometry (dim_t codim, dim_t i) const =0
	Construct a new Geometry() object that describes the geometry of the `i`-th sub-entity with codimension=`codim` More...

virtual std::vector< std::unique_ptr< Geometry > >	ChildGeometry (const RefinementPattern &ref_pat, lf::base::dim_t codim) const =0
	Generate geometry objects for child entities created in the course of refinement. More...

virtual bool	isAffine () const
	element shape by affine mapping from reference element More...

virtual	~Geometry ()=default
	Virtual destructor. More...

Private Attributes
Eigen::Matrix< double, Eigen::Dynamic, 3 >	coords_
	Coordinates of the 3 vertices/midpoints, stored in matrix columns. More...

Eigen::Matrix< double, Eigen::Dynamic, 1 >	alpha_

Eigen::Matrix< double, Eigen::Dynamic, 1 >	beta_

Eigen::Matrix< double, Eigen::Dynamic, 1 >	gamma_

double	alpha_squared_

double	alpha_beta_

double	beta_squared_

Additional Inherited Members
Public Types inherited from lf::geometry::Geometry
using	dim_t = base::RefEl::dim_t

Protected Member Functions inherited from lf::geometry::Geometry
	Geometry ()=default

	Geometry (const Geometry &)=default

	Geometry (Geometry &&)=default

Geometry &	operator= (const Geometry &)=default

Geometry &	operator= (Geometry &&)=default

Related Functions inherited from lf::geometry::Geometry
void	PrintInfo (std::ostream &o, const Geometry &geom, int output_ctrl=0)
	Diagnostic output operator for Geometry. More...

std::ostream &	operator<< (std::ostream &stream, const Geometry &geom)
	Operator overload to print a `Geometry` to a stream, such as `std::cout` More...

Detailed Description

A second-order segment in the plane or in 3D space.

Coordinates \( coords = [A, B, C] \) are mapped to the reference element as follows:

(0.0) - (0.5) - (1.0)        ->        A - C - B

Definition at line 25 of file segment_o2.h.

Constructor & Destructor Documentation

◆ SegmentO2()

lf::geometry::SegmentO2::SegmentO2 ( Eigen::Matrix< double, Eigen::Dynamic, 3 > coords )

explicit

Constructor building segment from vertex/midpoint coordinates.

Parameters

coords w x 3 matrix, w = world dimension, whose columns contain the world coordinates of the vertices/midpoints

Definition at line 15 of file segment_o2.cc.

References alpha_, alpha_beta_, alpha_squared_, beta_, beta_squared_, coords_, and gamma_.

Member Function Documentation

◆ ChildGeometry()

std::vector< std::unique_ptr< Geometry > > lf::geometry::SegmentO2::ChildGeometry	(	const RefinementPattern &	ref_pat,
		base::dim_t	codim
	)		const

overridevirtual

Generate geometry objects for child entities created in the course of refinement.

Parameters

ref_pat	An object encoding the details of refinement
codim	relative codimension of child entities whose shape is requested

Returns: an array of unique pointers pointers to geometry objects for child entities of the specified co-dimension and the given refinement pattern. The numbering of child entities is a convention.

Implementation of local mesh refinement entails splitting of elements into parts ("children"), whose shape will depend on the refinement pattern. This method creates the geometry objects describing the shape of children. The details of subdivisions corresponding to particular refinement patterns are fixed by the method RefinementPattern::ChildPolygons() and should be documented there.

See also: class lf::geometry::RefinementPattern

Implements lf::geometry::Geometry.

Definition at line 93 of file segment_o2.cc.

References lf::geometry::RefinementPattern::ChildPolygons(), Global(), lf::base::RefEl::kSegment(), lf::geometry::RefinementPattern::LatticeConst(), lf::geometry::RefinementPattern::NumChildren(), lf::geometry::RefinementPattern::RefEl(), and lf::base::RefEl::ToString().

◆ DimGlobal()

dim_t lf::geometry::SegmentO2::DimGlobal ( ) const

inlineoverridevirtual

Dimension of the image of this mapping.

Implements lf::geometry::Geometry.

Definition at line 35 of file segment_o2.h.

References coords_.

Referenced by JacobianInverseGramian().

◆ DimLocal()

dim_t lf::geometry::SegmentO2::DimLocal ( ) const

inlineoverridevirtual

Dimension of the domain of this mapping.

Implements lf::geometry::Geometry.

Definition at line 34 of file segment_o2.h.

◆ Global()

Eigen::MatrixXd lf::geometry::SegmentO2::Global ( const Eigen::MatrixXd & local ) const

overridevirtual

Map a number of points in local coordinates into the global coordinate system.

Parameters

local A Matrix of size DimLocal() x numPoints that contains in its columns the coordinates of the points at which the mapping function should be evaluated.

Returns: A Matrix of size DimGlobal() x numPoints that contains the mapped points as column vectors. Here numPoints is the number of columns of the matrix passed in the local argument.
\[ \mathtt{Global}\left(\left[\widehat{x}^1,\ldots,\widehat{x}^k\right]\right) = \left[ \mathbf{\Phi}_K(\widehat{x}^1),\ldots,\mathbf{\Phi}_K(\widehat{x}^k)\right]\;,\quad \widehat{x}^{\ell}\in\widehat{K}\;, \]
where \(\mathbf{\Phi}\) is the mapping taking the reference element to the current element \(K\).

This method provides a complete description of the shape of an entity through a parameterization over the corresponding reference element = parameter domain. The method takes as arguments a number of coordinate vectors of points in the reference element. For the sake of efficiency, these coordinate vectors are passed as the columns of a dynamic matrix type as supplied by Eigen.

For instance, this method is used in lf::geometry::Corners()

inline Eigen::MatrixXd Corners(const Geometry& geo) {

return geo.Global(geo.RefEl().NodeCoords()); }

lf::geometry::Geometry::Geometry

Geometry()=default

lf::geometry::Corners

Eigen::MatrixXd Corners(const Geometry &geo)

The corners of a shape with piecewise smooth boundary.

Definition: geometry_interface.h:261

Additional explanations in Lecture Document Paragraph 2.7.5.17.

Implements lf::geometry::Geometry.

Definition at line 31 of file segment_o2.cc.

References alpha_, beta_, and gamma_.

Referenced by ChildGeometry().

◆ IntegrationElement()

Eigen::VectorXd lf::geometry::SegmentO2::IntegrationElement ( const Eigen::MatrixXd & local ) const

overridevirtual

The integration element (factor appearing in integral transformation formula, see below) at number of evaluation points (specified in local coordinates).

Parameters

local A Matrix of size DimLocal() x numPoints that contains the evaluation points (in local = reference coordinates) as column vectors.

Returns: A Vector of size numPoints x 1 that contains the integration elements at every evaluation point.

For a transformation \( \Phi : K \mapsto R^{\text{DimGlobal}}\) with Jacobian \( D\Phi : K \mapsto R^{\text{DimGlobal} \times \text{DimLocal}} \) the integration element \( g \) at point \( \xi \in K \) is defined by

\[ g(\xi) := \sqrt{\mathrm{det}\left|D\Phi^T(\xi) D\Phi(\xi) \right|} \]

More information also related to the use of lovcal quadrature rules is given in Lecture Document Paragraph 2.7.5.24.

Implements lf::geometry::Geometry.

Definition at line 69 of file segment_o2.cc.

References alpha_beta_, alpha_squared_, and beta_squared_.

◆ Jacobian()

Eigen::MatrixXd lf::geometry::SegmentO2::Jacobian ( const Eigen::MatrixXd & local ) const

overridevirtual

Evaluate the jacobian of the mapping simultaneously at numPoints points.

Parameters

local A Matrix of size DimLocal x numPoints that contains the evaluation points as column vectors

Returns: A Matrix of size DimGlobal() x (DimLocal() * numPoints) that contains the jacobians at the evaluation points.

This method allows access to the derivative of the parametrization mapping in a number of points, passed as the columns of a dynamic matrix. The derivative of the parametrization in a point is a Jacobian matrix of size ‘DimGlobal() x DimLocal()’. For the sake of efficiency, these matrices are stacked horizontally and returned as one big dynamic matrix. Use Eigen's ‘block()’ method of Eigen::MatrixXd to extract the individual Jacobians from the returned matrix.

Implements lf::geometry::Geometry.

Definition at line 42 of file segment_o2.cc.

References alpha_, and beta_.

◆ JacobianInverseGramian()

Eigen::MatrixXd lf::geometry::SegmentO2::JacobianInverseGramian ( const Eigen::MatrixXd & local ) const

overridevirtual

Evaluate the Jacobian * Inverse Gramian ( \( J (J^T J)^{-1}\)) simultaneously at numPoints.

Parameters

local A Matrix of size DimLocal() x numPoints that contains the evaluation points as column vectors.

Returns: A Matrix of size DimGlobal() x (DimLocal() * numPoints) that contains the Jacobian multiplied with the Inverse Gramian ( \( J (J^T J)^{-1}\)) at every evaluation point.

Note: If DimLocal() == DimGlobal() then \( J (J^T J)^{-1} = J^{-T} \), i.e. this method returns the inverse of the transposed jacobian.

Example for recovering a single transposed inverse Jacobian.

If both dimensions agree and have the value D, then the method returns the transposed of the inverse Jacobians of the transformation at the passed points. These are square DxD matrices.

To retrieve the j-th inverse transposed Jacobian from the returned matrix, use the block methdod of Eigen (case (D = DimLocal()) == DimGlobal())

JacobianInverseGramian(local).block(0,i*D,D,D)

lf::geometry::SegmentO2::JacobianInverseGramian

Eigen::MatrixXd JacobianInverseGramian(const Eigen::MatrixXd &local) const override

Evaluate the Jacobian * Inverse Gramian ( ) simultaneously at numPoints.

Definition: segment_o2.cc:49

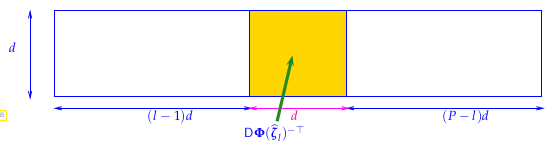
More explanations in Paragraph 2.8.3.14.

Implements lf::geometry::Geometry.

Definition at line 49 of file segment_o2.cc.

References alpha_, alpha_beta_, alpha_squared_, beta_, beta_squared_, and DimGlobal().

◆ RefEl()

base::RefEl lf::geometry::SegmentO2::RefEl ( ) const

inlineoverridevirtual

The Reference element that defines the domain of this mapping.

Implements lf::geometry::Geometry.

Definition at line 36 of file segment_o2.h.

References lf::base::RefEl::kSegment().

◆ SubGeometry()

std::unique_ptr< Geometry > lf::geometry::SegmentO2::SubGeometry	(	dim_t	codim,
		dim_t	i
	)		const

overridevirtual

Construct a new Geometry() object that describes the geometry of the i-th sub-entity with codimension=codim

Parameters

codim	The codimension of the sub-entity (w.r.t. `DimLocal()`)
i	The zero-based index of the sub-entity.

Returns: A new Geometry object that describes the geometry of the specified sub-entity.

Let \( \mathbf{\Phi} : K \mapsto \mathbb{R}^\text{DimGlobal} \) be the mapping of this Geometry object and let \( \mathbf{\xi} : \mathbb{R}^{\text{DimLocal}-codim} \mapsto K\) be the first-order mapping that maps the reference element RefEl().SubType(codim,i) to the i-th sub-entity of RefEl(). I.e. for every node \( \mathbf{n_j} \) of RefEl().SubType(codim,i) it holds that \( \mathbf{\xi}(\mathbf{n_j}) = \) RefEl().NodeCoords(RefEl().SubSubEntity2SubEntity(codim, i, DimLocal()-codim, j)).

Then the geometry element returned by this method describes exactly the mapping \( \mathbf{\Phi} \circ \mathbf{\xi} \)

Implements lf::geometry::Geometry.

Definition at line 81 of file segment_o2.cc.

References coords_.

Member Data Documentation

◆ alpha_

Eigen::Matrix<double, Eigen::Dynamic, 1> lf::geometry::SegmentO2::alpha_

private

Definition at line 65 of file segment_o2.h.

Referenced by Global(), Jacobian(), JacobianInverseGramian(), and SegmentO2().

◆ alpha_beta_

double lf::geometry::SegmentO2::alpha_beta_

private

Definition at line 74 of file segment_o2.h.

Referenced by IntegrationElement(), JacobianInverseGramian(), and SegmentO2().

◆ alpha_squared_

double lf::geometry::SegmentO2::alpha_squared_

private

Definition at line 73 of file segment_o2.h.

Referenced by IntegrationElement(), JacobianInverseGramian(), and SegmentO2().

◆ beta_

Eigen::Matrix<double, Eigen::Dynamic, 1> lf::geometry::SegmentO2::beta_

private

Definition at line 66 of file segment_o2.h.

Referenced by Global(), Jacobian(), JacobianInverseGramian(), and SegmentO2().

◆ beta_squared_

double lf::geometry::SegmentO2::beta_squared_

private

Definition at line 75 of file segment_o2.h.

Referenced by IntegrationElement(), JacobianInverseGramian(), and SegmentO2().

◆ coords_

Eigen::Matrix<double, Eigen::Dynamic, 3> lf::geometry::SegmentO2::coords_

private

Coordinates of the 3 vertices/midpoints, stored in matrix columns.

Definition at line 59 of file segment_o2.h.

Referenced by DimGlobal(), SegmentO2(), and SubGeometry().

◆ gamma_

Eigen::Matrix<double, Eigen::Dynamic, 1> lf::geometry::SegmentO2::gamma_

private

Definition at line 67 of file segment_o2.h.

Referenced by Global(), and SegmentO2().

The documentation for this class was generated from the following files:

/home/nico/bildung/SemVI/thesis/lehrfempp/lib/lf/geometry/segment_o2.h
/home/nico/bildung/SemVI/thesis/lehrfempp/lib/lf/geometry/segment_o2.cc

Public Member Functions

Private Attributes

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

◆ SegmentO2()

Member Function Documentation

◆ ChildGeometry()

◆ DimGlobal()

◆ DimLocal()

◆ Global()

◆ IntegrationElement()

◆ Jacobian()

◆ JacobianInverseGramian()

Example for recovering a single transposed inverse Jacobian.

◆ RefEl()

◆ SubGeometry()

Member Data Documentation

◆ alpha_

◆ alpha_beta_

◆ alpha_squared_

◆ beta_

◆ beta_squared_

◆ coords_

◆ gamma_